Resumen 02 / 05 / 2016
TIPOS DE PREGUNTAS PARA CUESTIONARIO DE ENCUESTAS.
- Según la contestación que admita el encuestado: Se opción abierta o múltiple.
Estas preguntas tiene como dificultad la tabulación de los resultados, ya que depende del encuestado.
- Según la naturaleza de contenido: preguntas sobre echos objetivos.
Preguntas de identificación especialmente.
- Según su función: de filtro, de consistencia y control, de aflojamiento y control.
Preguntas de filtro: Selecciona una parte de los encuestados para la realización de preguntas.
Preguntas de consistencia y control: Comprueban la congruencia de las respuestas.
Preguntas de aflojamiento: Establece el ambiente cómodo para el encuestado.
Resumen 04 / 05 / 2016
ESTADÍSTICA DESCRIPTIVA
1.-Recopilación de datos.
Resumen 04 / 05 / 2016
ESTADÍSTICA DESCRIPTIVA
1.-Recopilación de datos.
-Fuente
-Criterios para diseñar la encuesta
- Tema
- Problema (marco teórico)
- Objetivo general y objetivos específicos.
- Justificación y Referencias (normas APA)
- Tipos de datos.
-Cualitativos o Categóricos.
-Cuantitativos o numéricos (Discretos:datos individuales y Continuos: agrupados dentro de un intervalo)2.-Simbologia.
N= Tamaño de la Naturaleza.
n= Tamaño de la muestra.
X= Características de interés.
x= El valor de la característica.3.-Descripción del conjunto de datos.
4.- Tablas de frecuencias.
- Tabular.
- Gratificar.
- Números que caracterizan al conjunto de datos.
1.Identificar la unidad de medida de los datos.
2.Obtener el Rango de los datos. (R= Xmax - X min)
3.Seleccionar el numero de clases o también llamados intervalos (k)
n k
<50 5-7
50-100 6-10
100-250 7-12
>250 10-20
4.Longitud de la clase.5.-Realizar el conteo de datos para obtener la frecuencia en cada clase.
6.-Organizar la información en la tabla de frecuencias.
Resumen 09 / 05 / 2016
Ejercicio en clase

Ejercicio en clase de datos cualitativos y categóricos



Resumen 11 / 05 / 2016
Polígono de frecuencias:
Es el gráfico de línea que se diseña utilizando en
el eje horizontal la marca de clase de cada intervalo de una distribución de
frecuencias (marca de clase = punto medio). La información que se gráfica en un polígono puede ser absoluta o
relativa. Algunas de sus principales características son:
- En el eje horizontal se colocan las marcas de clase de cada intervalo
- En el eje vertical se ubica la frecuencia absoluta o la frecuencia porcentual
- Todos los puntos tienen la misma distancia en el eje X
- Las líneas siempre permanecen unidas
- Ambos extremos deben terminar sobre el eje horizontal
- Sólo funciona con datos numéricos o continuos
- En el cambio de intervalo se puede colocar la frecuencia absoluta o relativa para mayor comprensión de los datos.
Ejercicio
El peso de 65 personas adultas
viene dado por la siguiente tabla:
fuente: http://www.vitutor.net/2/11/poligonos_frecuencia.html. (definición y características)
fuente: http://www.vitutor.net/2/11/poligonos_frecuencia.html ( ejemplo y gráficos)
fuente: http://www.vitutor.net/2/11/poligonos_frecuencia.html ( ejemplo y gráficos)
Ojiva como gráfico estadística:
Es
un gráfico de línea que se diseña utilizando en el eje horizontal las fronteras
superiores de una distribución de frecuencias. La información se obtiene de la
columna de frecuencias acumuladas (absoluta o relativa). Las características
son las siguientes:
- En el eje horizontal se colocan las fronteras superiores de cada intervalo
- Todos los puntos tienen la misma distancia en el eje X
- Las líneas permanecen unidas
- El primer extremo termina sobre el eje horizontal
- Los datos son numéricos o continuos
- En el cambio de intervalo es posible colocar el valor de la frecuencia absoluta o relativa para una mejor comprensión de los datos.
La
forma general de una ojiva es la siguiente:
fuente: http://lbanegas.com/lecciones/capitulo02/capitulo0203.html
Diagrama de puntos:
Los diagramas de puntos sirven para presentar gráficamente tablas en las cuales se consideran únicamente una variable y una cantidad asociada a cada valor de la misma.
Hay dos tipos de diagramas de puntos. Los dos muestran esencialmente la misma información, sólo que en diferente forma y con diferente propósito. La construcción de estos diagramas se describe a continuación:
a) El primer tipo de diagrama de puntos se construye colocando en el eje horizontal los valores de la variable (los cuales en muchos casos son arbitrarios) y en el eje vertical las cantidades asociadas a éstos. Finalmente, para cada valor de la variable y cada cantidad asociada se dibujan puntos cuya altura corresponde a la magnitud de dicha cantidad.
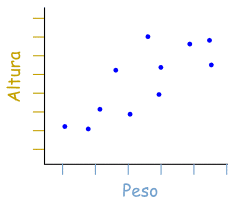
Gráfico: (ejemplo de el peso de un grupo de perdonas y su altura.)
b) Para construir el segundo tipo de diagramas de puntos se colocan en el eje horizontal los valores de la variable y sobre cada valor se dibujan tantos puntos como aparecen éstos
Gráfico: (calificaciones de un grupo de estudiantes)
fuente: http://colposfesz.galeon.com/est501/distfrec/metgraf/metgraf.htm
Diagrama de Tallo y Hojas:
Un diagrama donde cada valor de datos es dividido en una "hoja" (normalmente el último dígito) y un "tallo" (los otros dígitos). Por ejemplo "32" sería dividido en "3" (tallo) y "2" (hoja). Los valores del "tallo" se escriben hacia abajo y los valores "hoja" van a la derecha (o izquierda) del los valores tallo. El "tallo" es usado para agrupar los puntajes y cada "hoja" indica los puntajes individuales dentro de cada grupo.
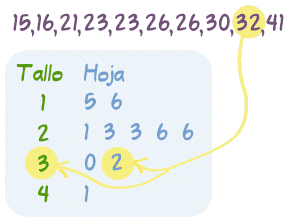
fuente: http://www.disfrutalasmatematicas.com/definiciones/diagrama-de-tallo-y-hojas.html
Diagrama de Pareto:
El Diagrama de Pareto consiste en un gráfico de barras similar al histograma que se conjuga con una ojiva o curva de tipo creciente y que representa en forma decreciente el grado de importancia o peso que tienen los diferentes factores que afectan a un proceso, operación o resultado.
fuente: http://www.monografias.com/trabajos47/diagrama-pareto/diagrama-pareto.shtml#ixzz4DJcPC6SI
* De localización:
Diagrama de puntos:
Los diagramas de puntos sirven para presentar gráficamente tablas en las cuales se consideran únicamente una variable y una cantidad asociada a cada valor de la misma.
Hay dos tipos de diagramas de puntos. Los dos muestran esencialmente la misma información, sólo que en diferente forma y con diferente propósito. La construcción de estos diagramas se describe a continuación:
a) El primer tipo de diagrama de puntos se construye colocando en el eje horizontal los valores de la variable (los cuales en muchos casos son arbitrarios) y en el eje vertical las cantidades asociadas a éstos. Finalmente, para cada valor de la variable y cada cantidad asociada se dibujan puntos cuya altura corresponde a la magnitud de dicha cantidad.

Gráfico: (ejemplo de el peso de un grupo de perdonas y su altura.)
b) Para construir el segundo tipo de diagramas de puntos se colocan en el eje horizontal los valores de la variable y sobre cada valor se dibujan tantos puntos como aparecen éstos
Gráfico: (calificaciones de un grupo de estudiantes)
fuente: http://colposfesz.galeon.com/est501/distfrec/metgraf/metgraf.htm
Diagrama de Tallo y Hojas:
Un diagrama donde cada valor de datos es dividido en una "hoja" (normalmente el último dígito) y un "tallo" (los otros dígitos). Por ejemplo "32" sería dividido en "3" (tallo) y "2" (hoja). Los valores del "tallo" se escriben hacia abajo y los valores "hoja" van a la derecha (o izquierda) del los valores tallo. El "tallo" es usado para agrupar los puntajes y cada "hoja" indica los puntajes individuales dentro de cada grupo.

fuente: http://www.disfrutalasmatematicas.com/definiciones/diagrama-de-tallo-y-hojas.html
Diagrama de Pareto:
El Diagrama de Pareto consiste en un gráfico de barras similar al histograma que se conjuga con una ojiva o curva de tipo creciente y que representa en forma decreciente el grado de importancia o peso que tienen los diferentes factores que afectan a un proceso, operación o resultado.
fuente: http://www.monografias.com/trabajos47/diagrama-pareto/diagrama-pareto.shtml#ixzz4DJcPC6SI
Resumen 16 / 05 / 2016
Se realizo la primera actividad en clase, ademas de la revisión de los cuestionarios acerca del tema de investigación
(enlace de la actividad en clase resuelta en clase)
Resumen 18 / 05 / 2016
Calculo de Medidas
- Media Muestral ( M )
- Mediana Muestral ( Me )
- Moda ( Mo )
- Rango ( R )
- Varianza ( S^2 )
- Desviación típica ( S )
- Coeficiente de Variación ( V )
- Cuartiles ( Qi )
- Deciles ( Di )
- Percentiles ( Pi )
- Asimetría ( As )
- Apuntamiento ( Ap )
Nota: Estas medidas solo se aplican para datos cuantitativos.
1) Medidas de Localización
- Datos agrupados en intervalos
La media muestral de datos agrupados por intervalos no es mas que la sumatoria de la marca de clase (punto medio) multiplicada por la frecuencia de cada intervalo, todo esto dividido para el numero de elementos.
MEDIANA MUESTRAL
- Datos individuales
- Datos individuales con frecuencia
La mediana muestral de los datos individuales con frecuencia, se calcula dividiendo e numero de elementos a la mitad, luego se analiza en que frecuencia acumulada se encuentra este resultado, el dato al que perteece dicha frecuencia absoluta es el que representa la mediana muestral.
- Datos agrupados en intervalos
 |
MODA
2) Medidas de Dispersión
RANGO
El rango es el mismo para cualquier tipo de datos, ya sean estos individuales o agrupados por intervalos
VARIANZA
- Datos individuales
- Datos individuales con frecuencia
- Datos agrupados en intervalos
La Varianza para datos agrupados en intervalos es la sumatoria de la marca de clase menos la media, todo esto elevado al cuadrado y luego multiplicado para la frecuencia de cada intervalo, multiplicado por el inverso de (n-1) donde n es el numero de elementos total.
X representa la media muestral.
DESVIACIÓN TÍPICA
La desviación típica es la raíz cuadrada de la varianza. Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
COEFICIENTE DE VARIACIÓN
Resumen 23 / 05 / 2016
3) Medidas de posición
Las medias de posición dividen un conjunto de datos en grupos con el mismo numero de individuos. Para calcular las medidas de posición es necesario que los datos estén ordenados de menor a mayor. Las medidas de posición son:
CUARTILES
Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.
Q1, Q2 y Q3 determinan los valores correspondientes al 25, 50 y al 75 de los datos. ademas Q2 coincide con la mediana.
Calculo de los Cuartiles
Calculo de los Cuartiles para datos Agrupados
Ejercicio
DECILES
Los deciles son los nueve valores que dividen la serie de datos en diez partes iguales.
Los deciles dan los valores correspondientes al 10%, al 20%... y al 90% de los datos.
D5 coincide con la mediana.
PERCENTILES
Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales.
Los percentiles dan los valores correspondientes al 1%, al 2%... y al 99% de los datos.
P50 coincide con la mediana.
P50 coincide con D5.
Resumen 25 / 05 / 2016
4) Medidas de Forma
Coeficiente de simetríaAsimetría Negativa o a la Izquierda.- Se da cuando en una distribución la minoría de los datos está en la parte izquierda de la media. Este tipo de distribución presenta un alargamiento o sesgo hacia la izquierda, es decir, la distribución de los datos tiene a la izquierda una cola más larga que a la derecha. También se dice que una distribución es simétrica a la izquierda o tiene sesgo negativo cuando el valor de la media aritmética es menor que la mediana y éste valor de la mediana a su vez es menor que la moda.
Nota: Sesgo es el grado de asimetría de una distribución, es decir, cuánto se aparta de la simetría.
Simétrica.- Se da cuando en una distribución se distribuyen aproximadamente la misma cantidad de los datos a ambos lados de la media aritmética. No tiene alargamiento o sesgo. Se representa por una curva normal en forma de campana llamada campana de Gauss (matemático Alemán 1777-1855) o también conocida como de Laplace (1749-1827).También se dice que una distribución es simétrica cuando su media aritmética, su mediana y su moda son iguales.
Asimetría Positiva o a la Derecha.- Se da cuando en una distribución la minoría de los datos está en la parte derecha de la media aritmética. Este tipo de distribución presenta un alargamiento o sesgo hacia la derecha, es decir, la distribución de los datos tiene a la derecha una cola más larga que a la izquierda.
También se dice que una distribución es simétrica a la derecha o tiene sesgo positivo cuando el valor de la media aritmética es mayor que la mediana y éste a valor de la mediana a su vez es mayor que la moda.
Resumen 30 / 05 / 2016
FUNDAMENTOS DE LA TEORÍA DE LA PROBABILIDAD
En esta unidad se revisan algunas definiciones
necesarias para fundamentar el estudio de la Teoría de la Probabilidad.
FÓRMULAS DE CONTEO
En esta sección revisamos algunas fórmulas básicas para conteo de los
elementos de grupos.
Principio Básico del Conteo
Si un grupo tiene m
elementos y otro grupo tiene n elementos, entonces existen mxn
formas diferentes de tomar un elemento del primer grupo y otro elemento del
segundo grupo.
Ejercicio. Se lanzan
un dado y una moneda. ¿Cuantos resultados diferentes se obtienen en este experimento?
Al lanzar el dado se pueden tener m = 6 resultados
diferentes, mientras que al lanzar la moneda se obtienen n = 2
resultados diferentes. Por lo tanto, el número total de resultados del
experimento es mxn = 6x2 = 12. El conjunto de resultados
posibles es:
{(1, c), (1, s), (2, c), (2, s), (3, c), (3, s),
(4, c), (4, s), (5, c), (5, s), (6, c), (6, s)}, c:
cara, s: sello
PERMUTACIONES
Son los arreglos diferentes que se pueden hacer con los elementos de un
grupo. En estos arreglos se debe considerar el orden de los elementos
incluidos. Suponga un conjunto de n elementos diferentes, del cual se toma un arreglo de r elementos.
Número
de permutaciones
Número de permutaciones con n elementos
diferentes de un conjunto del cual se toman arreglos conteniendo r elementos: nPr =
n(n-1)(n-2). . .(n-r+1)
Ejercicio . Un grupo de 10 personas debe elegir a su
directiva; presidente, secretario, tesorero. Todos pueden ser elegidos,
pero una persona no puede tener más de un cargo. ¿De cuantas maneras diferentes
puede realizarse la elección? (Use la fórmula de permutaciones)
Los arreglos posibles son permutaciones pues el orden
en cada uno si es de interés. Por lo tanto
n = 10, r = 3, 10P3 = 10x9x8 = 720
PERMUTACIONES CON ELEMENTOS REPETIDOS
Si del total de n elementos, n1 fuesen repetidos, entonces los arreglos tendrían
formas idénticas cuando se considera el orden de los n1 elementos repetidos. Existen n1! formas de tomar
los n1 elementos repetidos, por lo tanto, la cantidad de
permutaciones se reduciría por el factor n1!
Cantidad
de permutaciones con elementos repetidos = n! / n1 !




























No hay comentarios:
Publicar un comentario